Heterogeneous Models
Heterogeneous Models
The research unit features three different physical scenarios of heterogeneous physical models which share many modeling aspects and numerical requirements and serve as role models for a wider range of applications. We will briefly introduce these scenarios below.
Magnetized Plasma
This scenario is part of the wider field of models of magnetohydrodynamics
Goedbloed, Keppens, Poedts (2019), in which an electrically conducting fluid interacts with magnetic fields. It is one of the most
fundamental examples of a coupling between fluid flow and electrodynamics. The fluid experiences
the electromagnetic fields, while the motion of the fluid influences the evolution of the fields. Typically,
the fluid follows the equations of continuum mechanics, which include a mass-, momentum- and
energy-balance, and possibly viscous and heat-conducting effects. The electrodynamic fields follow
from the Maxwell equations. Between both these systems momentum- and energy-exchange takes
place, such that conservation of these quantities only makes sense for the system as a whole, see
Project B1, where in addition the evolution of entropy is considered.
The situation gets more involved through the fact that both the fluid and electrodynamics can be modeled by different descriptions. The charged particles may be considered as single quasi-neutral fluid or separated into independent species with different charges, see Project A2. The Maxwell equations could be used in eddy current formulation or full form including all electromagnetic waves. In certain regimes, the fluid particles must be described by kinetic theory using, for instance, the Vlasov equation Nicholson (1983), see Project B2, or by a moment hierarchy Zhdanov (2002), see Project B4. In all these formulations, conservation properties need to be clarified.
Complex Fluids
This scenario shows in its coupling patterns a striking similarity to magnetized
plasmas. Typically, complex fluids consider a suspension of mesoscopic particles, like macromolecules
or nano-particles, in a liquid. Here, we will consider a model of particles with rod-like
microscopic structure that is described in a configuration space of orientation or angle Doi, Edwards (1986). The
particles move with the liquid and change their orientation through the flow. In return, the particles
impose forces onto the liquid which are modeled as internal friction of the fluid. This process is
described by a kinetic equation for the distribution of orientation coupled to the liquid velocity. Again,
there is momentum and energy exchange and the conservation properties must be formulated for
the entire system.
Compared with the Vlasov-Maxwell system, this setting is slightly simpler (Vlasov’s velocity space is all \(R^3\), while orientation is \(S^2\)) and will also serve as a test compound for numerical strategies. Additionally, the kinetic description of the particles can be replaced by a moment hierarchy, see Project B3. Different flow regimes may require locally different moment descriptions. This extends the discussion to structural properties like conservation or entropy laws.
Electrochemical Systems
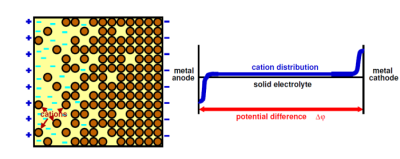This scenario requires more development in terms of modeling before
numerical methods can be applied, and also reaches out to diffusive rather than convection-dominated
processes. We consider Maxwell’s equations of electrodynamics coupled to a multicomponent,
non-neutral, possibly polarizable and magnetizable material
De Groot, Mazur (1962),
Dreyer, Guhlke, Müller (2013),
Griffith, Peskin (2013),
Mirabella (2010).
In this case, thDe Groot, Mazur (1962)e diffusion contains intriguing cross effects in which electric fields generate
diffusion fluxes and vice versa. The consistent modeling poses the question how the constitutive
relations of polarization and magnetization of a multi-component system interact with momentum
and energy conservation and an entropy law.
The focus of research will be on the appropriate formulation of the model equations, and to identify
the relevant structural elements that a numerical coupling procedure will be based on. This includes
the proper momentum and energy exchange mechanisms and an H-theorem, see Project A1, but
also multi-scale aspects and suitable model hierarchies, see Project A3.
