Extended-version

Extended-version

Principal Investigator:
Rainer Grauer, Theoretical Physics I, Ruhr-University Bochum

Main Collaborators in the Research Unit:
Gregor Gassner, Department of Mathematics and Computer Science, University of Cologne
Manuel Torrilhon, Applied and Computational Mathematics, RWTH Aachen
Eric Sonnendrücker, Computational Plasma Physics, IPP MPI & TU Munich

Coupling the two-fluid/Maxwell system to Magnetohydrodynamics/Ohm's law

The Need for Understanding the Transition from Maxwell's Equation to Ohm's Law

One of the main challenges in astrophysical, space and fusion plasmas is the treatment of different spatial and temporal scales and the correct physical description on each of these different scales. To give a rough estimate for different plasma systems, consider the warm ionized phase (diffusely ionized hydrogen) in the interstellar medium. Here the smallest relevant kinetic scales are in the order of kilometers, while the global scale of the system is about \(10^{13}\) km. In the heliosphere the scales are smaller overall (kinetic scales about 2 km, system scale about \(10^{8}\) km), but the ratio of global to kinetic scales is still astronomical in the truest sense of the word. The situation is similar for fusion plasmas: the electron skin depth is about 0.0005 m and the vessel measures about 10 meters. In all these cases it is not possible to perform simulations that represent all scales with the finest level (kinetic equations) of physical description. The plasmas under consideration are basically collisionless. An estimate of the typical mean free path in space plasmas is about 1 AU (\(\approx\) distance sun \(\leftrightarrow\) earth). Such collisionless plasmas can be modelled with the kinetic Vlasov equation. Nevertheless, kinetic models are inherently computationally expensive, so that large-scale simulations of typical phenomena, as for example magnetic reconnection or collisionless shocks, are hardly feasible and only possible in localized regions of interest. As an alternative, cheaper fluid models can be considered, but they lack the expressiveness and some physics of full of kinetic models. The maximum entropy approach to distribution functions has been shown in McDonald, Torrilhon (2013) to be a very accurate approximation method. This approach is described in detail in project B4. The development of a fluid description for collisionless plasmas on kinetic scales based on this approach is one of our future goals. That this is a very desirable goal was demonstrated in Ng, Hakim, Bhattacharjee (2018). In this paper, the electron distribution function obtained from Vlasov simulations was projected onto the maximum entropy approach. The non-Maxwellian features of the distribution function were remarkably well captured by this ansatz. Fluid descriptions can be easily obtained by taking moments of the distribution function: multiplying by powers of \(\mathbf{v}\) and integrating over the velocity space leads to expressions for particle density \(n_{s}(\mathbf{x}, t)=\int f_{s}(\mathbf{x}, \mathbf{v}, t) \mathrm{d} \mathbf{v}\), mean velocity \(\mathbf{u}_{s}(\mathbf{x}, t)=\frac{1}{n_{s}(\mathbf{x}, t)} \int \mathbf{v} f_{s}(\mathbf{x}, \mathbf{v}, t) \mathrm{d} \mathbf{v}\), pressure \(\mathrm{P}_{s}=m_{s} \int \mathbf{v}^{\prime} \otimes \mathbf{v}^{\prime} f_{s} \mathrm{~d} \mathbf{v}\) and heat flux \(\mathrm{Q}_{s}=m_{s} \int \mathbf{v}^{\prime} \otimes \mathbf{v}^{\prime} \otimes \mathbf{v}^{\prime} f_{s} \mathrm{~d} \mathbf{v}\). Here, \(\otimes\) is the tensor product and \(\mathbf{v}^{\prime}=\mathbf{v}-\mathbf{u}\).

A fluid description that is still capable of describing certain effects on kinetic scales (e.g., electron skin depth \(d_e\), electron gyroradius \(\rho_e\)) is the 10-moment two-fluid model

\[ \begin{align} &\frac{\partial n_{s}}{\partial t}+\nabla \cdot\left(n_{s} \mathbf{u}_{s}\right)=0 \\ &m_{s} \frac{\partial\left(n_{s} \mathbf{u}_{s}\right)}{\partial t}=n_{s} q_{s}\left(\mathbf{E}+\mathbf{u}_{s} \times \mathbf{B}\right)-\nabla \cdot \mathcal{P}_{s} \\ &\frac{\partial \mathcal{P}_{i j}^{s}}{\partial t}-q_{s}\left(n_{s} u_{[i}^{s} E_{j]}+\frac{1}{m_{s}} \epsilon_{[i k l} \mathcal{P}_{k j]}^{s} B_{l}\right)=-\left(\nabla \cdot \mathcal{Q}_{s}\right)_{i j} \; , \end{align}\]

where \(\mathcal{P}_{s}=m_{s} \int \mathbf{v} \otimes \mathbf{v} f_{s} \mathrm{~d} \mathbf{v}\) and \(\mathcal{Q}_{s}=m_{s} \int \mathbf{v} \otimes \mathbf{v} \otimes \mathbf{v} f_{s} \mathrm{~d} \mathbf{v}\) are the second and third moments of the distribution function (multiplied by mass), \(\epsilon_{i k l}\) is the Levi-Civita symbol and the square brackets denote the sum over as many permutations of indices as needed to make the tensors symmetric (e.g. \(u_{[i} E_{j]}=u_{i} E_{j}+u_{j} E_{i}\)). The electromagnetic fields \(\boldsymbol{E}\), \(\boldsymbol{B}\) evolve through Maxwell's equations,

\[ \begin{align} &\partial_{t} \mathbf{E}=c^{2}\left(\nabla \times \mathbf{B}-\mu_{0} \mathbf{j}\right) & \nabla \cdot \mathbf{E}=\frac{\rho}{\varepsilon_{0}} \\ &\partial_{t} \mathbf{B}=-\nabla \times \mathbf{E} & \nabla \cdot \mathbf{B}=0 \, , \end{align}\]

the current density \(\boldsymbol{j}=\sum_{s} q_{s} \mathbf{u}_{s}\) being obtained from the fluid equations acting as a source term Allmann-Rahn, Trost, Grauer (2018). Treatments and modeling of Landau damping (for a physics discussion, see Chust, Belmont, Mottez, Hess (2009) and for a mathematical treatment consult Mouhot, Villani (2011) implemented as heat flux closures have been proposed and analyzed in Wang, Hakim, Bhattacharjee, Germaschewski (2015), [Allmann-Rahn, Trost, Grauer (2018)]https://doi.org/10.1017/S002237781800048X). These studies were based on the closure introduced by Hammett, Perkins (1990) and successive works in this direction Hammett, Dorland, Perkins (1992), Passot, Sulem (2003). An extension providing heat flows in the parallel and perpendicular directions (with respect to the magnetic field) was presented in Sharma, Hammett, Quataert (2003). Excellent overviews are given in Chust, Belmont (2006), Hunana, Tenerani et al. (2019). Using such an Hammett-Perkins type Landau damping heat flux closure Allmann-Rahn, Lautenbach, Grauer, Sydora (2021) instabilities like the lower hybrid drift and firehose instabilities could be captured and their significance in reconnection scenarios could be highlighted.

An even simpler description can be obtained by assuming an isotropic temperature resulting in the 5-moment two-fluid description. In order to ease the later discussion on magnetohydrodynamic (MHD) we adapt the normalization used in Ho, Datta, Shumlak (2018) \(\epsilon_{0}=\frac{e^{2} n_{0}}{m_{0} \omega_{p}^{2}}\), \(\mu_{0}=\frac{B_{0}^{2}}{m_{0} n_{0} V_{A}^{2}}\), \(E_{0}=v_{0} B_{0}\), \(v_{0}=\frac{L}{\tau}=V_{A}\) with ion cyclotron frequency \(\omega_{c}=\frac{e B_{0}}{m_{p}}\). Relating the ion cyclotron frequency to the ion skin depth results in \(\omega_{c} \tau = \frac{L}{d_{i}}\) and the 5 moment two fluid equations take the form

\[ \begin{align} &\frac{\partial \rho_{\alpha}}{\partial t}+\nabla \cdot \boldsymbol{p}_{\alpha}=0 \\ &\frac{\partial \boldsymbol{p}_{\alpha}}{\partial t}+\nabla \cdot\left(\frac{\boldsymbol{p}_{\alpha} \otimes \boldsymbol{p}_{\alpha}}{\rho_{\alpha}}+P_{\alpha} \stackrel{\leftrightarrow}{\boldsymbol{I}}\right)=\left(\frac{L}{\delta_{p}}\right)\left(\frac{Z_{\alpha}}{A_{\alpha}}\right)\left(\rho_{\alpha} \boldsymbol{E}+\boldsymbol{p}_{\alpha} \times \boldsymbol{B}\right) \\ &\frac{\partial e_{\alpha}}{\partial t}+\nabla \cdot\left(\left(e_{\alpha}+P_{\alpha}\right) \frac{\boldsymbol{p}_{\alpha}}{\rho_{\alpha}}\right)=\left(\frac{L}{\delta_{p}}\right)\left(\frac{Z_{\alpha}}{A_{\alpha}}\right) \boldsymbol{p}_{\alpha} \cdot \boldsymbol{E} \end{align}\]

where the electromagnetic fields still evolve by Maxwell's equations, which in this normalization read

\[ \begin{align} &-\frac{1}{\left(\omega_{p} \tau\right)^{2}}\left(\frac{L}{\delta_{p}}\right)^{2} \frac{\partial \boldsymbol{E}}{\partial t}+\nabla \times \boldsymbol{B}=\left(\frac{L}{\delta_{p}}\right) \boldsymbol{j} \; , \;\; & \frac{1}{\left(\omega_{p} \tau\right)^{2}} \frac{L}{\delta_{p}} \nabla \cdot \boldsymbol{E}=\rho_{c} \\ &\frac{\partial \boldsymbol{B}}{\partial t}+\nabla \times \boldsymbol{E}=0 \; , \;\; & \nabla \cdot \boldsymbol{B}=0 \end{align}\]

Here \(Z_\alpha\) denotes the ionization state and \(A_\alpha\) the atomic mass. This normalization allows to identify the correspondence of \(\mu_{0}\) to the Alfvén velocity as well as the relation of \(\epsilon_{0} \rightarrow 0\) as \(c \rightarrow \infty\) or \(\omega_{p} \rightarrow \infty\), resulting in a vanishing displacement current. In addition to the assumption of isotropy of the electron and ion distribution functions, the heat flux is neglected here if the distribution functions are assumed to be close to Maxwellian. However, the 5-moment two-fluid model is still capable of capturing separate electron and ion motions and thus inertia effects, hall currents and thus whistler waves as well as electromagnetic waves.

Probably the best known description on large spatial and temporal scales (compared to ion kinetic scales) in astrophysical, space, and fusion plasmas is magnetohydrodynamics (MHD), equipped with a generalized Ohm's law that prescribes the electric field \(\boldsymbol{E}\).

In this project, we will focus on the coupling to the two-temperature MHD equations

\[ \begin{aligned} &\frac{\partial \rho}{\partial t}+\nabla \cdot \boldsymbol{p}=0 \\ &\frac{\partial \boldsymbol{p}}{\partial t}+\nabla \cdot\left(\frac{\boldsymbol{p} \otimes \boldsymbol{p}}{\rho}-\boldsymbol{B} \otimes \boldsymbol{B}+\left(P+\frac{\boldsymbol{B} \cdot \boldsymbol{B}}{2}\right) \stackrel{\leftrightarrow}{\boldsymbol{I}}\right)=0 \\ &\frac{\partial e_{\alpha}}{\partial t}+\nabla \cdot\left(\left(e_{\alpha}+P_{\alpha}\right) \frac{\boldsymbol{p}_{\alpha}}{\rho_{\alpha}}\right)=\left(\frac{L}{\delta_{p}}\right)\left(\frac{Z_{\alpha}}{ A_{\alpha}}\right) \boldsymbol{p}_{\alpha} \cdot \boldsymbol{E} \, . \end{aligned}\]

The magnetic and electric fields are governed by Faraday's law and a generalized Ohm's law (which includes electron pressure and the Hall term)

\[ \begin{aligned} &\frac{\partial \boldsymbol{B}}{\partial t}+\nabla \times \boldsymbol{E}=0 \\ &\rho \boldsymbol{E}+\boldsymbol{p} \times \boldsymbol{B}=\left(\frac{A_{i}}{Z_{i}}\right)\left(\left(\frac{\delta_{p}}{L}\right) \nabla P_{e}+\boldsymbol{j} \times \boldsymbol{B}\right) \, . \end{aligned}\]

There are much more complete versions of Ohm's law (see e.g. Baumjohann, Treumann (1996)). The meaning of each of these additional terms contributing to the total electric field has been analyzed with incredible precision using the data from the NASA's Magnetospheric Multiscale (MMS) mission Stawarz, Matteini et al. (2020).

Particularly revealing is Fig. 2 in their paper, which clearly shows that the contribution of the ideal MHD term to the electric field \(\mathbf{E}_\text{MHD}=-\mathbf{u} \times \mathbf{B}\) is dominant on scales larger than the ion gyroradius, as expected. By almost two orders of magnitude smaller are the contributions of the Hall term \(\mathbf{E}_\text{Hall}=\frac{1}{e n} \mathbf{j} \times \mathbf{B}\) and the electron pressure \(\mathbf{E}_{P_e}=\frac{1}{e n} \nabla \cdot {\overleftrightarrow{P}}_{e}\). Important to note is that the electron pressure term gets more and more important below the ion skin depth \(d_i\). The contributions of inertial terms or finite electron mass corrections are then four orders of magnitude smaller on length scales above the ion gyroradius. The upshot of this detailed analysis is that coupling an MHD description with the 5-moment two-fluid description is possible if no ion-scale phenomena are relevant in the intended MHD range.

Fortunately, for many relevant problems, such as magnetic reconnection or collisionless shocks, there is a fairly clear separation of scales and regimes, so an adaptive approach is promising and could combine the best of both worlds: cheap models where they are sufficient and detailed models where they are necessary and interesting.

A sketch of the just described hierarchy is depicted in the Figure below Lautenbach, Grauer (2018). In the inner zone, both ions and electrons are treated kinetically and solved with the Vlasov equation. Adjacent to this zone, ions are still modelled with the Vlasov equation but electrons are described with a 10-moment fluid model. On the next coarser level of description, the ions are also described by a 10-moment fluid model. To ease the transition from the kinetic to the 10-moment fluid description we apply the Landau closure developed in Allmann-Rahn, Trost, Grauer (2018) in the fluid description.

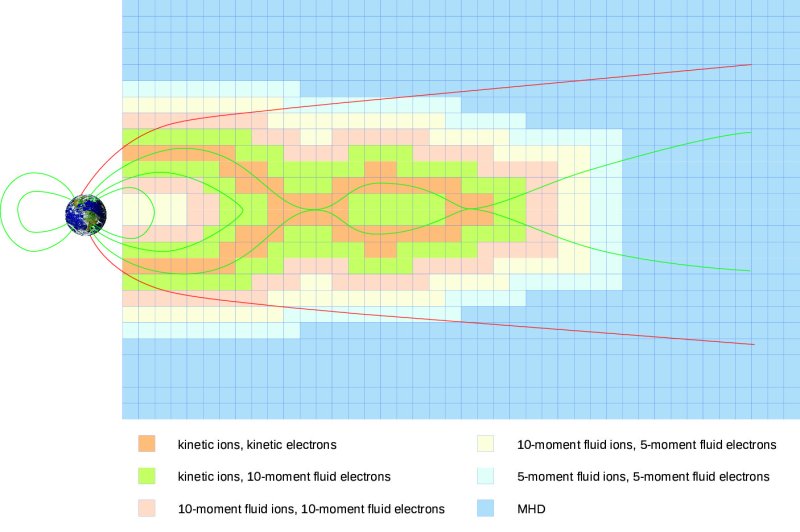
It may turn out that in some spatial regions outside the reconnection zone the temperature tensor in the 10-moment description is nearly isotopic. In this case it is even possible to switch to a 5-moment description. This change can be done separately for ions and electron. Vlasov, 10- and the 5-moment models are coupled to Maxwell's equation. The coupling of the 5-moment model to MHD (with generalized Ohms law) represent the last step in this hierarchy. This step is of utmost importance because in many space plasma scenarios the spatial domain where MHD description can be relied upon and applied is by far the largest in volume.

Interface Coupling of MHD/Ohm's Law With a Two-Fluid/Maxwell System

The interface-coupling of MHD/generalized Ohm's law with a two-fluid/Maxwell description is a challenging project due to the singular limits involving the speed of light \(c\) approaching infinity (compared to the Alfvén speed) (or the vacuum permittivity \(\epsilon_0\) approaching zero) and at the same time reaching quasi-neutrality in the plasma. These limits imply modeling issues, e.g how to deal with fast light waves and/or plasma Langmuir waves that are not included in the MHD plasma description. Quasi-neutrality demands for recipes on how to obtain the electric field and relate it to the electric field in Maxwell's equation. Closely related to this is the issue of energy conservation. Energy is defined differently in the two systems; in particular, MHD does not include electric field contributions to the energy. Thus, the question naturally arises how to treat the contributions of fast light and Langmuir waves at interfaces (reflections) and how to formulate the corresponding interface fluxes (required in finite volume, discontinuous Galerkin, and active flux methods) in the absence of information on electron quantities. A further major challenge is the formulation of physically and mathematically justified refinement criteria to decide when a model change from MHD to the two-fluid/Maxwell system and vice versa must be carried out.

Kinetic to Fluid Coupling

Multi-physics techniques and the idea of coupling different physical models is not new and has been applied in different physical contexts. Schulze et al. Schulze, Smereka, E (2003) couple kinetic Monte-Carlo and continuum models in the context of epitaxial growth. Quite some substantial efforts has been undertaken to couple kinetic Boltzmann descriptions to fluid models (see e.g. Le Tallec, Mallinger (1997), Tiwari, Klar (1998), Klar, Neunzert, Struckmeier (2000), Degond, Dimarco, Mieussens (2010), Dellacherie (2003), Goudon, Jin et al. (2013) Tiwari, Klar et al. (2013). Kolobov and Arslanbekov Kolobov, Arslanbekov (2012) described the transition from neutral gas models to models of weakly ionized plasmas.

In the context of space plasma physics, Sugiyama, Kusano (2007) have begun coupling MHD and particle-in-cell (PIC) models and tested this approach on a 1D Alfvén wave test problem where the MHD and PIC regions were fixed in advance. Markidis, Henri et al. (2014) introduce a bulk coupling of a 4-moment two-fluid/Maxwell solver with an embedded PIC code. The PIC code is used to calculate the closure for the stress and pressure tensors. To achieve the large time steps compatible with the MHD description, an implicit Maxwell solver is used. Daldorff, Toth et al. (2014) introduced interface coupling to combine kinetic PIC simulations (using the implicit iPIC3D code) with Hall MHD fluid codes (using the BATS-R-US framework). A closely related approach is presented in Makwana, Keppens, Lapenta (2017) using MPI-AMRVAC as the MHD solver. This strategy was applied to global simulations of the magnetotail Walker, Lapenta et al. (2019), with the slight modification of only one-sided coupling of the MHD with the PIC solver. The feedback effect of the PIC simulation on the MHD fluid quantities was neglected. Also worth mentioning is the multi-level multi-domain method for Particle-In-Cell simulations Innocenti, Lapenta et al. (2013), which bypasses the reshaping of weight functions in adaptive PIC simulations. Implicit time integration is important in these treatments, such that fast waves, e.g., light, Langmuir, Whistler, and electron drift waves, are damped.

Asymptotic-Preserving Strategies for Plasma Flows

Asymptotic preserving (AP) methods have quite a long history and tradition in fluid dynamics, e.g., the AP scheme for kinetic-fluid modeling of two-phase flows Goudon, Jin et al. (2013) mentioned earlier or schemes related to radiation/kinetic transport phenomena Krycki, Berthon et al. (2013), Laiu, Frank, Hauck (2019).

Degond et al. Degond, Deluzet, Doyen (2017), Degond, Deluzet (2017) studied the transition of the Vlasov-PIC system to the quasi-neutral limit in the case of a fixed ion background density. They consider an expansion in \(\lambda = \frac{\lambda_D}{L}\), where \(\lambda_D\) denotes the Debye length and \(L\) is the system scale, to construct a suitable semi-implicit AP scheme. Their work also gives a partial justification for other implicit methods. It is worth mentioning that their method allows to calculate the irrotational part of the electric field \(\mathbf{E}\), which is underdetermined in the naive limit.

In a recent study Crestetto, Deluzet, Doyen (2020) the method was extended for bridging kinetic plasma descriptions and single-fluid models. In addition to the former treatment, the authors introduce additional expansion parameters that control the limit to various fluid approximations.

The well-known Darwin approximation of Maxwell's equations (PIC: Nielson, Lewis (1976), Vlasov Schmitz, Grauer (2006)) can also be seen as part of the AP strategy. A systematic derivation of a hierarchy of approximations for Maxwell's equations can be found in Raviart, Sonnendruecker (1996).

Slow Manifold Approach to MHD

Burby (2017) raised the important question of why the MHD description appears to remain valid in situations where relaxation to a Maxwell distribution is not assured due to the absence or smallness of possible dissipation mechanisms (including kinetic ones). He uses that in an appropriate scaling the two-fluid/Maxwell system corresponds to a fast-slow system and that the MHD dynamics evolves on an invariant slow submanifold in the larger space of fast and slow motions. Thus, if one starts with initial conditions on this slow manifold so that no \"fast\" degrees of freedom are excited, the evolution stays on this manifold. A functional differential equation makes it possible to find approximate equations for the dynamics on the slow manifolds.

In a recent work Miloshevich, Burby (2021), the extension of a reduction of the Vlasov/Maxwell system to an evolution on a (dark = non-radiating) slow manifold was presented.

Conservative and Non-Conservative Coupling

Ho, Datta, Shumlak (2018) presented a detailed study and numerical tests on the coupling of the 5-moment fluid/Maxwell and the MHD model. They discuss the issue of interface fluxes in the transition from the MHD to the two-fluid model. The difficulty lies in the lack of information on electron quantities. Two approaches have been presented to obtain this missing information. The first leads to conservative fluxes, while the second is physically consistent with the MHD assumptions. The interesting observation was that conservative coupling leads to oscillations, while physically consistent but not conservative coupling leads to a stable scheme. This work raises the question of which structures must be preserved in the interfacial coupling problem.

Some related work

In our group, we have quite a long history in developing codes and in plasma simulations using the MHD and Hall-MHD models in various applications, e.g., formation of strong current sheets Grauer, Marliani (2000), Effenberger, Thust et al. (2011), expanding flux ropes and coronal mass ejections Arnold, Dreher, Grauer et al. (2008), Fichtner, Kopp et al. (2008), Kleimann, Kopp et al. (2009), singularity formation and filamentation, Dreher, Ruban, Grauer (2005), Dreher, Laveder, et al. (2005) as well as whistler wave propagation using a physics based preconditioning for an implicit treatment of the Hall-MHD system Arnold, Dreher, Grauer (2008).

We also gained experience on the kinetic treatment of magnetic reconnection Schmitz, Grauer (2006a) using a semi-Lagrangian treatment of the Vlasov equation. For the Lagrangian treatment, we developed the backsubstitution method Schmitz, Grauer (2006b) in accordance with the Darwin's approach for Maxwell's equation to avoid propagation of light waves Schmitz, Grauer (2006c).

Our group has also recognized experience in the development of numerical methods that focus specifically on the multi-scale and multi-physics challenges as well as high performance computing (HPC) issues. Multi-scale challenges using block-structured adaptive mesh refinement (AMR) was addressed in Kleimann, Kopp et al. (2004), Dreher, Grauer (2005). HPC issues were also addressed in Arnold, Beetz et al. (2007). The framework racoon is a massive parallel tree based AMR code which scales linearly up to more than 200.000 processors on the BlueGene architecture (see figure below). racoon has also been used to study singular structures in the incompressible Euler equations Grafke, Grauer (2013), Grafke, Grauer (2013b) related to the Clay Millenium problem on global existence for the incompressible Navier-Stokes equations.

To address multi-physics problems, we have developed the framework MuPhy Rieke, Trost, Grauer (2015) Lautenbach, Grauer (2018). MuPhy allows the dynamic adaptive coupling of different models (e.g. 5-moment, 10-moment, kinetic Vlasov description) according to the underlying local plasma parameters (see figure below). The code is highly parallelized and capable of running on a cluster of CUDA graphics cards.

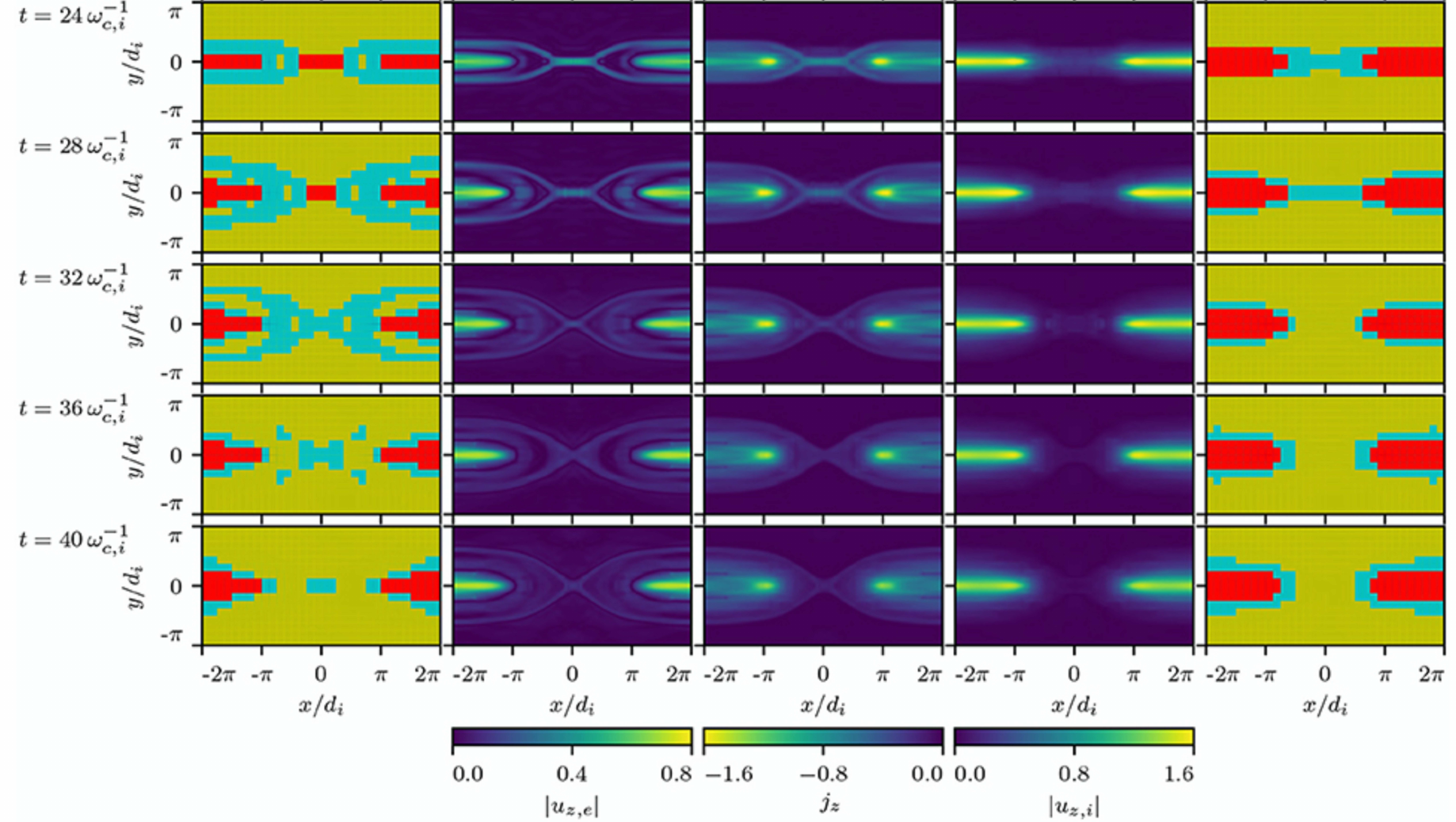
\(\left|u_{z, e}\right|, j_{z}\) and \(\left|u_{z, i}\right|\) for different times in units of the inverse ion gyro frequency \(\omega_{c, i}^{-1} .\) On the outsides, the preferred models are depicted based on the values of \(u_{z, s}\). Red areas are solved with the kinetic solver, blue areas with the ten-moment, and yellow areas with the five-moment fluid solver. Figure taken from Lautenbach, Grauer (2018).

The movie below shows the adaptive change of the different models in time.

MuPhy was used in Allmann-Rahn, Trost, Grauer (2018), Allmann-Rahn, Lautenbach, Grauer, Sydora (2021) to study reconnection scenarios. A detailed comparison to MMS data is presented in Allmann-Rahn, Lautenbach, Grauer (2021). The HPC experience we gained during the development of racoon, as well as the computational strategies developed in MuPhy for multi-physics problems, will strongly influence the future roadmap of Trixi.jl.

The next steps

The long-term goal of this project is to integrate the interface coupling of the 2 fluid/Maxwell system with the MHD modeling into a global hierarchical multi-physics description of collisionless space plasmas. This coupling, which is the goal of this project, is of great importance because the MHD modeling takes up the largest volume fraction in such a global simulation.The numerical challenges arise from the three singular limits for the MHD approximation: the speed of light \(c\) tends to infinity, the Debye length \(\lambda\) and the mass ratio \(\frac{m_e}{m_i}\) tend to zero. The modeling and numerical difficulties lead to the formulation of the following objectives:

• Develop a consistent transition from the two-fluid/Maxwell description to the MHD/Ohm's law model by understanding which structures need to be preserved.
  Here we mean, for example, what is meant by conservation of energy of the system when the energy in the MHD system does not include the electric field component? Or does it make sense to define conservative fluxes for the electrons if this information is hidden in Ohm's law?

• Use this knowledge to derive coupling strategies including the definition of consistent refinement criteria.
  The expansions used in the asymptotic preserving schemes presented Degond, Deluzet, Doyen (2017), Crestetto, Deluzet, Doyen (2020) and in the slow manifold approach Burby (2017) will guide us to define conservative fluxes both for the missing electron fluid variables as well as the projection on the slow Maxwell variables.

• The full chain from MHD/generalized Ohm's law \(\longrightarrow\) two fluid/Maxwell \(\longrightarrow\) Vlasov/Maxwell is envisaged.
  This is of course the final goal to realize global simulations from kinetic to MHD scales - e.g. for magnetotail reconnection.

Plasma Interactions Cardiology Models