Extended-version
Extended-version
Principal Investigators:
Rainer Grauer, Theoretical Physics I, Ruhr-University Bochum
Christiane Helzel, Applied Mathematics, Heinrich-Heine-University
Main Collaborator in the Research Unit:
Michael Schlottke-Lakemper, High-Performance Computing Center
Stuttgart, University of Stuttgart
An Active Flux Method for the Vlasov-Maxwell system
The Vlasov/Maxwell System
In this project we consider the Vlasov/Maxwell system for a collisionless plasma, which constitutes a prototype demanding system for structure-preserving bulk coupling. Most space and astrophysical plasmas can be considered as collisionless. An estimate of the typical mean free path in space plasmas is about 1 AU (\(\approx\) distance sun \(\leftrightarrow\) earth). Such collision-free plasmas are described with the kinetic Vlasov equation, which is coupled to Maxwell's equations. Both equations, the Vlasov equation and Maxwell's equation, are themselves linear. The bulk coupling of both set of equations, which describe the interaction of particles and the electromagnetic fields, make this complex system a great challenge for numerics and a problem of highest computational expense. Therefore, there is a special demand for precise but also extremely effective numerical descriptions for the integration of the Vlasov/Maxwell system.
The mathematical model consists of the kinetic Vlasov equation
\[ \begin{aligned} \label{B2:eqn:Vlasov} \partial_t f_s + \boldsymbol{v} \cdot \nabla_{\boldsymbol{x}} f_s + \frac{q_s}{m_s} \left( \boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B} \right) \cdot \nabla_{\boldsymbol{v}} f_s = 0, \end{aligned}\]
where \(f_s = f_s(\boldsymbol{x},\boldsymbol{v},t)\) is a probability density function of species \(s\), which depends on time \(t\), macroscopic space \(\boldsymbol{x} \in \mathbb{R}^d\) and the particle velocity \(\boldsymbol{v} = \boldsymbol{v}(\boldsymbol{x},t) \in \mathbb{R}^d\). The Vlasov equation is a transport equation in \((\boldsymbol{x},\boldsymbol{v})\) space. The particles are coupled indirectly through the electromagnetic fields. \(\boldsymbol{B}=\boldsymbol{B}(\boldsymbol{x},t) \in \mathbb{R}^d\) is the magnetic field and \(\boldsymbol{E}=\boldsymbol{E}(\boldsymbol{x},t) \in \mathbb{R}^d\) is the electric field. We denote with \(q_s\) and \(m_s\) the charge and mass of particles of species \(s\) (electrons: \(s=e\), ions: \(s=i\)).
The electromagnetic field satisfies Maxwell's equation, which consist of the dynamic evolution equations
\[ \begin{aligned} \label{B2:eqn:Maxwell} \partial_t \boldsymbol{B} & = - \nabla \times \boldsymbol{E} \\ \partial_t \boldsymbol{E} & = c^2 \left( \nabla \times \boldsymbol{B} - \mu_o \boldsymbol{j} \right) \end{aligned}\]
and the constraints
\[ \begin{aligned} \label{B2:eqn:constraints} \nabla \cdot \boldsymbol{E} & = \frac{\rho}{\epsilon_0}, \ \nabla \cdot \boldsymbol{B} = 0. \end{aligned}\]
Here \(\mu_0\) is the vacuum permeability, \(\epsilon_0\) is the vacuum permittivity and \(c\) is the speed of light. They satisfy the equation \(1/c^2 = \mu_0 \epsilon_0\). Furthermore, \(\rho\) is the total charge density and \(\boldsymbol{j}\) is the total current density computed via
\[ \begin{aligned} \label{B2:eqn:rho_j} \rho := \sum_s q_s n_s, \quad \boldsymbol{j} := \sum_s q_s n_s \boldsymbol{u}_s. \end{aligned}\]
The computation of the quantities \(\rho\) and \(\boldsymbol{j}\) requires moments of \(f_s\), namely
\[ \begin{aligned} n_s(\boldsymbol{x},t) & := \int_{\mathbb{R}^d} f_s(\boldsymbol{x},\boldsymbol{v},t) \, d\boldsymbol{v} & &\mbox{particle density of species $s$}\\ \boldsymbol{u}_s (\boldsymbol{x},t) & := \frac{1}{n_s(\boldsymbol{x},t)}\int_{\mathbb{R}^d} \boldsymbol{v} f_s(\boldsymbol{x},\boldsymbol{v},t) \, d\boldsymbol{v} & &\mbox{bulk velocity of species $s$}. \end{aligned}\]
Thus, the solution of the kinetic Vlasov equation directly influences the electromagnetic fields via the source term \(\boldsymbol{j}\).
The Vlasov/Maxwell system has been used in numerous simulations of space and astrophysical plasmas, as well as in simulations of laboratory experiments (see Palmroth, Ganse, Pfau-Kempf et al. (2018), Allmann-Rahn, Lautenbach, Grauer (2021), Nishikawa, Duţan et al. (2021) to name a few).
The numerical simulation of the Vlasov/Maxwell system is challenging for several reasons:
-
The Vlasov equation is high dimensional (6 dimensions in position and velocity phase space + time), thus numerical simulations are computationally expensive.
-
Although the Vlasov equation has the form of a relatively simple transport equation, the advection velocity \(\boldsymbol{v}\) might have very large components, which can lead to severe time step restrictions. Furthermore, explicit computations of Maxwell's equation require timesteps which resolve the speed of light \(c\).
-
The distribution function \(f_s\) needs to be positive and conserved. Conservation in \(f_s\) can easily be obtained by using a finite volume method or a discontinuous Galerkin method. To maintain positivity a limiter will in general be necessary.
-
From a conservative approximation of \(f_s\) we obtain a conservative approximation of the continuity equations for the particle densities \(n_s\), but not necessarily for quantities associated with higher moments. For example, the total energy
\[ E_{Vlasov/Maxwell} := \sum_{s} \frac{m_{s}}{2} \int\int |\mathbf{v}|^{2} f_{s}(\mathbf{x}, \mathbf{v}, t) \mathrm{d} \mathbf{v}\mathrm{d} \mathbf{x} + \frac{1}{2} \int \left(\varepsilon_{0}|\mathbf{E}|^{2}+\frac{1}{\mu_{0}}|\mathbf{B}|^{2}\right)\mathrm{d} \mathbf{x}\]
must be constant in time. This needs to be included as an additional constraint in the discretization as, e.g., in Juno, Hakim et al. (2018). If, for example, information about the characteristics is used in the numerical procedure, then it must also be guaranteed that by the acceleration term \(\boldsymbol{v} \times \boldsymbol{B}\) no energy is added. This can be realized by some variant of a Boris step Ripperda, Bacchini et al. (2018). Otherwise, artificial heating of the distribution may result from numerical dissipation.
-
The numerical solution should satisfy the constraints \(\nabla \cdot \boldsymbol{E} = \frac{\rho}{\epsilon_0}\), \(\nabla \cdot \boldsymbol{B} = 0\).
Thus, an ideal scheme for the Vlasov/Maxwell system should be of high order with low dissipation and therefore little heating and also truly multi-dimensional.
In this project we want to achieve these goals by utilising an Active Flux method both for the Vlasov and the Maxwell part.
Brief Review of Numerical Methods
Numerical methods to solve the Vlasov equation range from Eulerian to semi-Lagrangian, from finite difference Qin, Shu (2011), finite volumes Filbet, Sonnendrücker, Bertrand (2001), discontinuous Galerkin (DG) Rossmanith, Seal (2011), Juno, Hakim, TenBarge, Shi, Dorland (2018)) to spectral methods Eliasson (2003), Delzanno (2015). In addition to these grid-based methods, particle approaches such as particle-in-cell (PIC) Arber, Bennett et al. (2015) or fast summation techniques Masek, Gibbon (2010) are well established.
All these methods have their own strengths and weaknesses that determine their applicability to a particular problem of plasma physics. Lagrangian schemes for the Vlasov equation offer the advantage that the characteristics can be easily calculated. However, the standard method for solving the Vlasov equation is the 6-dimensional splitting as it was introduced in Cheng, Knorr (1976). Unfortunately, large splitting errors may occur as demonstrated in Schmitz, Grauer (2006b) (see also Roe (2017)). To circumvent these splitting errors, the back-substitution method was introduced Schmitz, Grauer (2006b), Schmitz, Grauer (2006c). In summary, the major issues in Lagrangian schemes are large stencils for high-order schemes to minimize heating and the application of dimensional splitting.
Eulerian schemes are generally preferable if a collision term is included. A comparison of Eulerian and Lagrangian schemes is presented in Filbet, Sonnendrücker (2003). Eulerian schemes do not take full advantage of the simple advection form of the Vlasov equation. Thus dissipation is slightly enhanced compared to Lagrangian schemes which leads to unphysical heating of the system.
Additional complexity results from the interaction with the electromagnetic fields governed by Maxwell's equations. E.g., in order to fulfil the constraint \(\nabla\cdot\boldsymbol{B}=0\) in solving Maxwell's equations, most often a staggered Yee grid Yee (1966) for the magnetic field \(\boldsymbol{B}\) or cleaning methods are applied Powell (1994), Dedner, Kemm et al. (2002). Related methods adjusting directly the fluxes Torrilhon (2005) or working with the vector potential Helzel, Rossmanith, Taetz (2011), Helzel, Rossmanith, Taetz (2013) have previously been proposed by members of this research unit. Directly related to the \(\nabla\cdot\boldsymbol{B}=0\) constraint is the issue of charge conservation. The charge density obtained from the electric field in Maxwell's equations should equal the charge density obtained from the zeroth moment of the Vlasov equation, i.e. \(\nabla \cdot \boldsymbol{E} = \rho / \epsilon_0\) This affects the deposition of the current density \(\boldsymbol{j}\), which is used as source term in Maxwell's equations. Especially, it dictates the joint temporal discretization of Vlasov and Maxwell's equations. For particle-in-cell simulations, this issue is mainly resolved Esirkepov (2001) and also translated to the Vlasov case Umeda, Togano, Ogino (2009). The last reference serves as guideline in designing the combined Vlasov/Maxwell solver.
Finally, the Vlasov/Maxwell system has severe time-step limitations due to fast light waves, plasma oscillations with the plasma frequency \(\omega_{\mathrm{p}, s}=\sqrt{\frac{n_{s} e^{2}}{\varepsilon_{0} m_{s}}}\) and the fast electron dynamics due to the targeted realistic mass ratios. This can partially be overcome with sub-cycling approaches as used in Rieke, Trost, Grauer (2015), Lautenbach, Grauer (2018). An alternative are Paired-Runge-Kutta (PRK) approaches as the main subject in Project .
The Active Flux Method
The Active Flux method, introduced by Eymann and Roe Eymann, Roe (2011a), Eymann, Roe (2011b), Eymann, Roe (2013), is a third order accurate finite volume method for hyperbolic conservation laws, which is based on the use of point values as well as cell average values of the conserved quantities. The point values are updated using exact or approximative evolution formulas. The point values are located at the grid cell interfaces and serve as nodes of Simpson's quadrature formula which is used to compute the numerical fluxes. Furthermore, some of these point values are also used for the reconstruction as explained below.
Over the last years, Roe Roe (2017a) Roe (2017b), Roe2021 proposed to reconsider all main components of today's CFD codes. The goal is to construct truly multidimensional, high order accurate methods with a compact stencil in space and time. While the spatial locality of the Active flux method is comparable with DG methods, its compact stencil in time leads to better stability properties. We expect that the compact stencil in space and time will simplify the bulk coupling of the kinetic Vlasov equation with Maxwell's equation.
Several other authors have contributed to the development of the Active Flux method, see for example Barsukow, Hohm, Klingenberg, Roe (2019), Barsukow (2021), and our own contributions Helzel, Kerkmann, Scandurra (2019), Chudzik, Helzel, Kerkmann (2021). There is also earlier related work by Lukáčová-Medvid'ová et al., see for example Lukácˇová-Medvid’ová, Morton, Warnecke (2000), Lukácˇová-Medvid’ová, Saibertová, Warnecke (2002), in which exact multidimensional evolution operators have been used as building blocks of numerical schemes. Those methods differ from the Active Flux method mainly in the choice of the degrees of freedom.
In Helzel, Kerkmann, Scandurra (2019), we explored the connection between the Active Flux method and ADER methods. For special linear problems, the Active Flux method is equivalent with a special version of an ADER method. This led us to a concept that allows the extension of Active Flux methods to nonlinear problems. In Chudzik, Helzel, Kerkmann (2021), we studied the linear stability of the two-dimensional Cartesian grid Active Flux method for advection and acoustics. Furthermore, we proposed a limited reconstruction based on the concept of bound preserving limiters by Zhang and Shu Zhang, Shu (2011). In work with David Kerkmann (PhD 09/2021, HHU), see Helzel, Kerkmann (2020) and Kerkmann2021, we explored the use of the Active Flux method for the construction of Cartesian grid cut cell methods.
We will explain the basic ideas of the Active Flux method by considering the one-dimensional scalar conservation law
\[ \partial_t q(x,t) + \partial_x f(q(x,t)) = 0,\]
where \(q: \mathbb{R} \times \mathbb{R}^+ \rightarrow \mathbb{R}\) is the conserved quantity and \(f:\mathbb{R} \rightarrow \mathbb{R}\) is the flux function. For simplicity we use an equidistant grid with mesh width \(\Delta x\). The degrees of freedom of the Active Flux method are cell averaged values and point values of the conserved quantity, we use the notation
\[ Q_i^n \approx \frac{1}{\Delta x} \int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} q(x,t) dx, \, Q_{i+\frac{1}{2}}^n \approx q(x_{i+\frac{1}{2}},t_n).\]
In order to describe a single time step, we assume that we have third order accurate approximations \(Q_{i+\frac{1}{2}}^n\) and \(Q_{i}^n\) at time \(t_n\). The cell average of the conserved quantities is updated using the finite volume approach
\[ Q_i^{n+1} = Q_i^n - \frac{\Delta t}{\Delta x} \left( F_{i+\frac{1}{2}} - F_{i-\frac{1}{2}} \right),\]
where Simpson's rule is used to compute the numerical fluxes
\[ \begin{align} F_{i+\frac{1}{2}} & := \frac{1}{6} \left( f(Q_{i+\frac{1}{2}}^n) + 4 f(Q_{i+\frac{1}{2}}^{n+\frac{1}{2}}) + f(Q_{i+ \frac{1}{2}}^{n+1}) \right) \\ & \approx \frac{1}{\Delta t} \int_{t_n}^{t_{n+1}} f(q(x_{i+\frac{1}{2}},t)) dt. \end{align}\]
The crucial step is the computation of the point values \(Q_{i+\frac{1}{2}}^{n+\frac{1}{2}}\) and \(Q_{i+\frac{1}{2}}^{n+1}\). Eymann and Roe suggested to use exact evolution formulas, which are available for advection or acoustics. For nonlinear problems different approaches have been investigated, see Barsukow (2021), Helzel, Kerkmann, Scandurra (2019).
For the scalar advection equation, i.e. for \(f(q) = a q\), \(a \in \mathbb{R}\), the exact evolution formula is well known
\[ \begin{aligned} Q_{i+\frac{1}{2}}^{n+\frac{1}{2}} & \approx q(x_{i+\frac{1}{2}},t_{n+\frac{1}{2}}) = q(x_{i+\frac{1}{2}}-a \frac{\Delta t}{2},t_n )\\ Q_{i+\frac{1}{2}}^{n+1} & \approx q(x_{i+\frac{1}{2}},t_{n+1}) = q(x_{i+\frac{1}{2}}-a \Delta t,t_n ). \end{aligned}\]
However, the exact solution at time \(t_n\) is unknown and thus \(q(.,t_n)\) needs to be replaced by a reconstruction. The Active Flux method uses a continuous, piecewise quadratic reconstruction which is in each grid cell obtained from the two point values and the cell average value. A schematic description of the method is shown in the figure below.
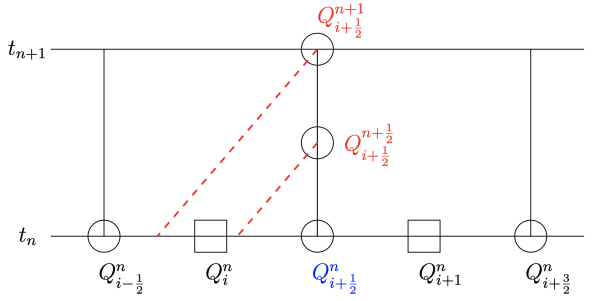
Eymann, Roe (2013) also proposed a two-dimensional version of the Active Flux method on triangular grids. Two-dimensional Cartesian grid versions have been used in Barsukow, Hohm, Klingenberg, Roe (2019), Helzel, Kerkmann, Scandurra (2019) and Chudzik, Helzel, Kerkmann (2021). In the two-dimensional Cartesian grid case we assume, that the cell average \(Q_{ij}^n\) of the conserved quantity in grid cell \((i,j)\) as well as all point values at cell corners, i.e. \(Q_{i\pm\frac{1}{2}, j\pm\frac{1}{2}}^n\) and edge midpoints \(Q_{i\pm \frac{1}{2},j}^n\) and \(Q_{i,j\pm\frac{1}{2}}^n\) are known at time \(t_n\). From these values a quadratic polynomial can be reconstructed which interpolates all the point values along the boundary and preserves the cell average. The numerical fluxes are again computed using Simpson's rule, now over a rectangle of size \(\Delta y \Delta t\) or \(\Delta x \Delta t\), respectively. The use of Simpson's rule again requires additional point values at time \(t_{n}+\frac{\Delta t}{2}\) and \(t_n + \Delta t\). As mentioned above, the Active Flux method in its original form uses exact evolution formulas to compute these point values. Such formulas are also available for advection and acoustics in higher dimensions, see for example Eymann, Roe (2013) For the two-dimensional advection equation
\[ \partial_t q + a \partial_x q + b \partial_y q = 0,\]
with \(q = q(t,x,y)\), \(q: \mathbb{R}^+ \times \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\) and \(a,b \in \mathbb{R}\), the evolution of the Active Flux method uses the simple relation
\[ q(t_n + \Delta t, x,y) = q(t_n,x-a\Delta t, y - b\Delta t)\]
for the update of the point values. For the two-dimensional acoustic equations
\[ \label{B2:eqn:acoustics} \begin{split} \partial_t p + c \nabla \cdot \boldsymbol{u} & = 0 \\ \partial_t \boldsymbol{u} + c \nabla p & = 0 \end{split}\]
the evolution is based on the spherical mean formula and can be found in Eymann, Roe (2013) and Barsukow, Hohm, Klingenberg, Roe (2019). Barsukow et al. Barsukow, Hohm, Klingenberg, Roe (2019). showed that their two-dimensional Cartesian grid Active Flux method for acoustics is stationary preserving and vorticity preserving. This property will be instrumental for our Active Flux Maxwell solver.
In recent work with PhD student Erik Chudzik (HHU), we have extended the two-dimensional Cartesian grid Active Flux method to a method that works on adaptively refined grids. The method has been implemented in ForestClaw, a parallel, adaptive library for solving PDEs on a hierarchy of logically Cartesian grids, developed by Calhoun and Burstedde Calhoun, Burstedde (2017), ForestClaw. The resulting method preserves the conservativity and third order accuracy of the Active Flux method. The figure below shows numerical results for the acoustic equations.

Some first results for the 1D1V Vlasov-Poisson Problem
Kinetic simulations based on discretizations of the Vlasov equation have a long tradition at TPI/RUB Schmitz, Grauer (2006b), Schmitz, Grauer (2006c), Rieke, Trost, Grauer (2015). An alternative to these direct simulations is the Particle in Cell (PIC) method (see for example Arber, Bennett et al. (2015) although both methods have their strengths and weaknesses. We focus on the direct method, since properties of the distribution function can be obtained much more accurately and also without noise. The movie below, in which isosurfaces of the electron distribution function are shown, serves as an example.
The movie displays different locations at a fixed time in a reconnection calculation and run from the inflow region via the reconnection X-point to the outflow region. In particular, the effect of electron inertia can be seen on the isosurfaces and also the rotation of the distribution function by the magnetic field. Furthermore, one can also see from such representations that at a sufficient distance from the X-point the distribution function approaches a Maxwell distribution. The previous semi-Lagrange finite volume method is based on the positive flux conservative method (PFC) Filbet, Sonnendrücker, Bertrand (2001) coupled with a finite-difference time-domain (FDTD) Maxwell solver Taflove (1995). It performs very stably and reliably, but shows numerical dissipation, which leads to numerical heating.
A key reason for using Active Flux methods for the approximation of the Vlasov/Maxwell system is that the evolution of the face-values is independent from the update of the cell averages. This gives the necessary freedom to use semi-Lagrangian ideas (such as the above-mentioned Boris step) for the evolution of face values. A crucial step will be the choice of the quadrature rule for the flux computation to achieve the above mentioned consistency of charge conservation.
In the context of a bachelor thesis by Lukas Hensel (2020) we have tried for the first time to apply the Active Flux method to the one-dimensional Vlasov-Poisson system (1d in real space, 1d in velocity space)
\[ \frac{\partial f_{s}}{\partial t}+{v} \cdot \frac{\partial f_{s}}{\partial {x}}+\frac{q_{s} }{m_{s}} {E}\, \frac{\partial f_{s}}{\partial {v}}=0 \, , \,\, \partial_{xx} \Phi = \frac{1}{\epsilon_{0}} \int \sum_s q_{s} f_{s} d v \; , \,\, {E}= -\partial_x \Phi \, .\]
This work was strongly inspired by the work of Maeng (2017) in the formulation using the bubble function approach.
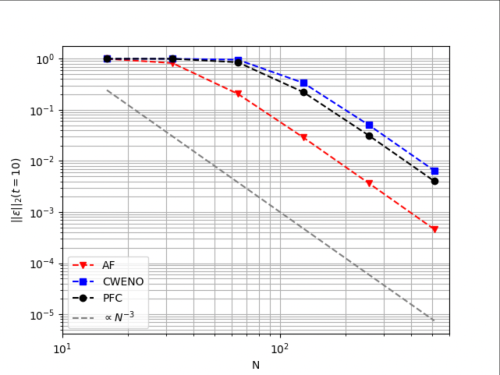
Lukas Hensel first studied linear 1d and 2d advection also using FCT limiters, which gave good results in one dimension, as expected. In the advection test case, the AF method was compared with the PFC method and a CWENO third-order finite volume scheme. All methods converge to third order, but from the preliminary studies so far, there is a clear advantage of the AF method as can be seen in the figure below
Next, the 1d Vlasov equation introduced before was solved in two different ways: i) with a Strang splitting for the spatial and velocity directions and for each of these directions a 1d AF method and ii) a 2d AF method for the whole phase space.
A comparison of the PFC method, the AF method with Strang splitting and the 2d AF method on the weak Landau damping test problem is shown in the figure below.
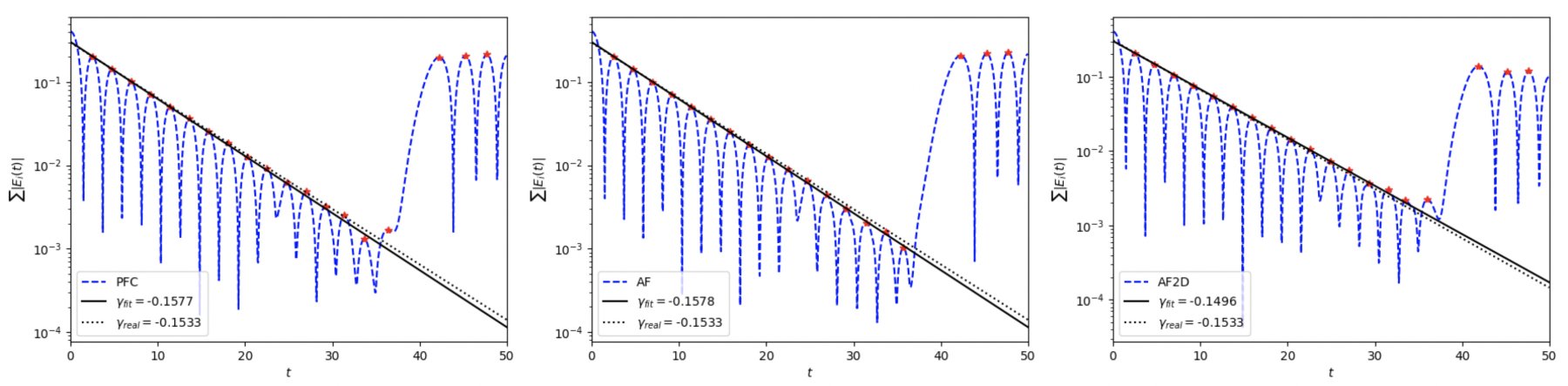
The results of all methods are very comparable in this example. In particular, the AF method in combination with a splitting method for the real and velocity space encourages a similar approach in the case of the 6d Vlasov/Maxwells system.
After his bachelor thesis and in preparation for his master thesis, Lukas Hensel continued to work on the AF method and implemented the so-called discrepancy distribution based on Bai, Roe (2021) for the 1d and 2d advection problem. The positive results of Bai, Roe (2021) could not be fully confirmed and need further clarification.
Lukas Hensel is currently working on 3D advection as a starting point for a 6D Vlasov-Poisson solver.
